Bugün siz değerli okuyucularıma kentsel ulaştırma ile ilgili paylaşımlarda bulunacağım. Ulaştırma politikası ve planlama kararları hemen hemen hayatın bütün aşamalarını etkilemektedir. Bu gibi kararlar birçok zaman, birbiriyle çelişen amaçlar arasında önem ve öncelik sırasına göre tercihi gerektirmektedir. Örneğin, araç seyahat hızlarını arttırmaya yönelik stratejiler, çarpışma risklerini arttırabilir ve yürüyüş standartlarını düşürebilir. Çeşitli emisyon azaltma stratejileri, araç fiyatlarını yükseltebilir yada toplam motorlu araç seyahatini düşürebilir. Otopark arzının arttırılması da konut fiyatlarını ve vergilerini arttırmaktadır. Bu gibi kararların değerlendirilmesi ve sayısallaştırılması için bir çatkının oluşturulması önemlidir. Araç işletim maliyetleri ve seyahat süresi değerleri gibi çeşitli ulaştırma etkileri, üzerinde yeterli çalışma yapıldığından ve büyüklüklerinin tahmini kolay olduğundan, bunlara bağlı değerlendirmeleri de kolaylıkla yapılabilir. Yaya yolu yürüme koşulları yada sera gazı salımındaki değişim gibi diğer etkilerin sayısallaştırılması daha zordur ve karar alıcılar tarafından çoğu zaman soyut etkiler olarak adlandırılıp somut etkilerden daha önemsiz görülür ve değerlendirmelerden çıkartılır.
Plan analizleri…
Bu kapsamda, geniş bir tercih aralığının değerlendirilmesinde rahat ve uyarlanabilir bir formatta fayda ve maliyet bilgilerinin sağlanmasında daha kapsamlı ulaştırma politika ve planlama analizlerine yoğunlaşılmalıdır. Bu çerçevede değişik ulaştırma türleri için bütün fayda ve maliyet hesaplarının geliştirilmesi için en uygulanabilir veriler kullanılmalıdır. Yayalar ve bisikletliler için aktif ulaştırma sağlık faydaları da hesaba dahil edilmiştir. Bu kapsamda üç farklı seyahat koşulu için (kentsel alanda pik saatler, kentsel alanda pik dışı saatler ve kırsal alan) 11 farklı ulaştırma türünde taşıt-mil ve yolcu-mil bazlı maliyet hesapları bulunmaktadır. Bu şekliyle kurulan analiz çatkısı, ulaştırma aktivitelerinin ve planlama seçeneklerinin karşılaştırmalı değerlendirmesini kolaylaştırmaktadır.
Bir kent oldukça karmaşık bir ulaştırma ağına sahiptir. Kent plancıları için hem mikro ve hem de makro ölçekte değerlendirme oldukça zor olduğundan bu çalışmaların çoğu ampirik olarak yapılmaktadır. Karayolu ağı değerlendirmesinde ilgili çalışmalar kapsamında yeni bir yöntem olarak Oransal Sürekli Kısmi Analiz ortaya konulmaktadır. Önceki araştırmalar kenti bir bütün olarak değerlendirmekte ve kentler arası kısmi analizler gerçekleştirmektedir. Söz konusu çalışmalarda ise kent, oranlı sürekli bir yüzey olarak ele alınmakta ve yüzeyin her bir parçasına kısmi analiz atamaktadır. Bilgisayarın çok uçlu yapısının gücü ve Coğrafi Bilgi Sistemleri (CBS) platformu sayesinde bu analizler birkaç saat içerisinde tamamlanabilmekte ve plancılara görsel sonuçlar aktarılabilmektedir. Diğer alt sistemlerle kıyas, plancılar ve politika yapıcılara kentlerin mevcut durumlarını sezgisel ve daha açık bir şekilde detaylı görüş imkanı sunmakta ve böylelikle çeşitli kararlar ve tahminleri kolaylıkla alabilmektedirler.
Bütünle benzerlik…
Klasik Öklidçi geometri, görsel uzayı tam sayılı olarak tanımlamakta olup böylelikle uzayda düzenli, ideal bir mevcudiyet ya da bunlardan mürekkep bir mevcudiyet söz konusu olmaktadır. Örneğin CAD platformunda çizgiler, kurblar, dikdörtgenler, kutular, silindirler ve diğer basit geometrik şekiller Öklid geometrisine göre çizilebilmektedir. Dağlar, bulutlar, ağaçlar ve kar gibi çeşitli doğal nesneler ifade edilmek istendiğinde bu daha karmaşık bir durum ortaya koyacaktır. Bu düzensiz nesneler olabildiğince büyütülebilmeli ve her birisi bütünle benzerlik gösterebilmelidir. Bu gibi nesnelerin CAD’da bütün detaylarının tanımlanması mümkün değildir. Uygulamada ne kadar detay ifade edilmek isteniyorsa o kadar çok sayıda çokgen kullanılmaktadır. Çokgenlerin sayısı ne kadar incelenmek ve ölçülendirmek istendiğine bağlıdır. 1967’de kısmi ölçeklendirmenin konu edildiği bir çalışmada sahil şeridinin uzunluğunu ölçülmesi, ölçek büyüklüğüne bağlı olarak sınanmış olup bu da bir paradoksu göstermektedir. Ampirik olaraksa daha küçük olan, ölçüdeki artışı, daha büyük olan ise ölçülen uzunluğu göstermektedir. Aynı zamanda ölçülen uzunluğun (L(G)) ölçü biriminin (G) bir fonksiyonu olduğu da gözlemlenmiştir.
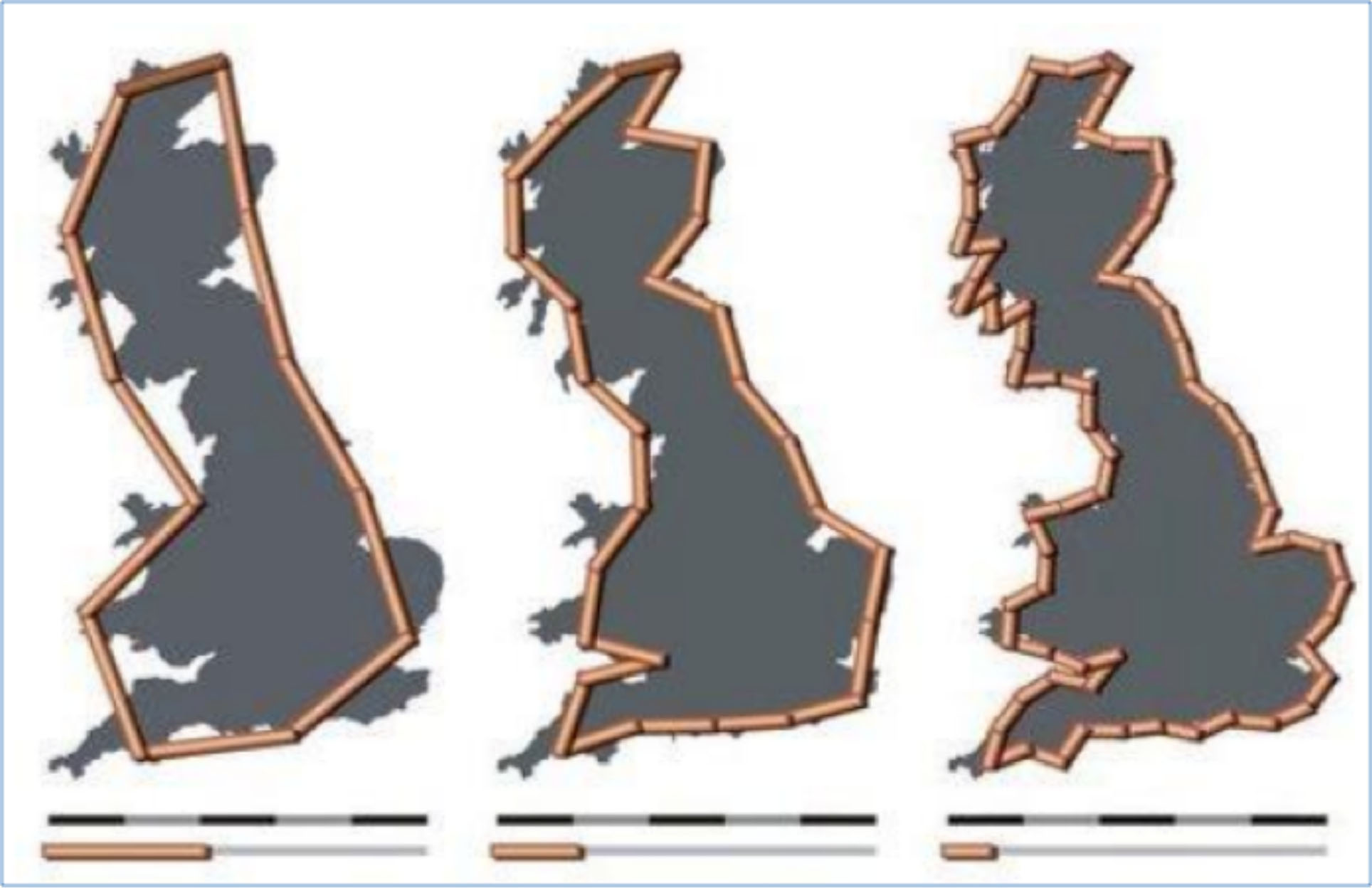

Şekil 1. Küçük Olan, Ölçekteki Artış, Büyük Olan İse Ölçülen Uzunluktur
Kısmi Karakteristikleri ve Kentler
Çok sayıda kısmi yaklaşım olup temel kısmi karakteristikler aşağıdaki gibidir:
• Kısmi çözümler pürüzsüz değildir, her yerde kesikli çizgilerle ifade edilmektedir. Bu da bu çözümlerin Öklid geometrisinde bütünüyle ölçülendirilemeyeceği anlamına gelmektedir.
• Kısmi çözümlemeler kendine özgüdür. Kısmi çözümlemelerin parçaları, bütününe benzemekte olup bir ölçekten diğerine benzer düzensizlikleri taşımaktadır. Bu yolla; kısmi çözümlemeler, karakteristik parçalarının hiyerarşisine göre de tanımlanabilmektedir. Kısmi çözümlemelerde 3 tür kendine benzerlik bulunmaktadır: tam kendine benzerlik, yarı kendine benzerlik ve istatistiksel kendine benzerlik.
• Kısmi çözümlemeler oldukça karmaşıktır. Bu; çizim büyütmelerinin git gide daha fazla detayı ortaya çıkaracağı anlamına gelmektedir. Bazı kısmi çözümlemeler ise iterasyonlarla geliştirilmektedir. Şekil 2’de tipik bir kısmi çözümleme olan Mandelbrot dizisi gösterilmektedir. Yukarıda belirtilen karakteristikler bu dizi üzerinde açıkça görülebilmektedir.
• Bir kısmi çözümleme; kısmi ölçeklerle ölçülebilir. Bu tam sayılı olmayan parametre, bir kısmi çözümleyicinin pürüzlülük derecesini sınamak için sıklıkla kullanılmaktadır. Bir sahil şeridi, verili 1 ve 2 noktaları arasındaki kısmi bir ölçüye sahip olabilmektedir. Eğer bir çizgi kadar pürüzsüzse kısmi ölçü 1’e yakınsayacaktır. Eğer her yere kıvrılabiliyor ve bir yüzeyi kaplayabilecek kadar karmaşıksa, 2’ye yakınsayacaktır.
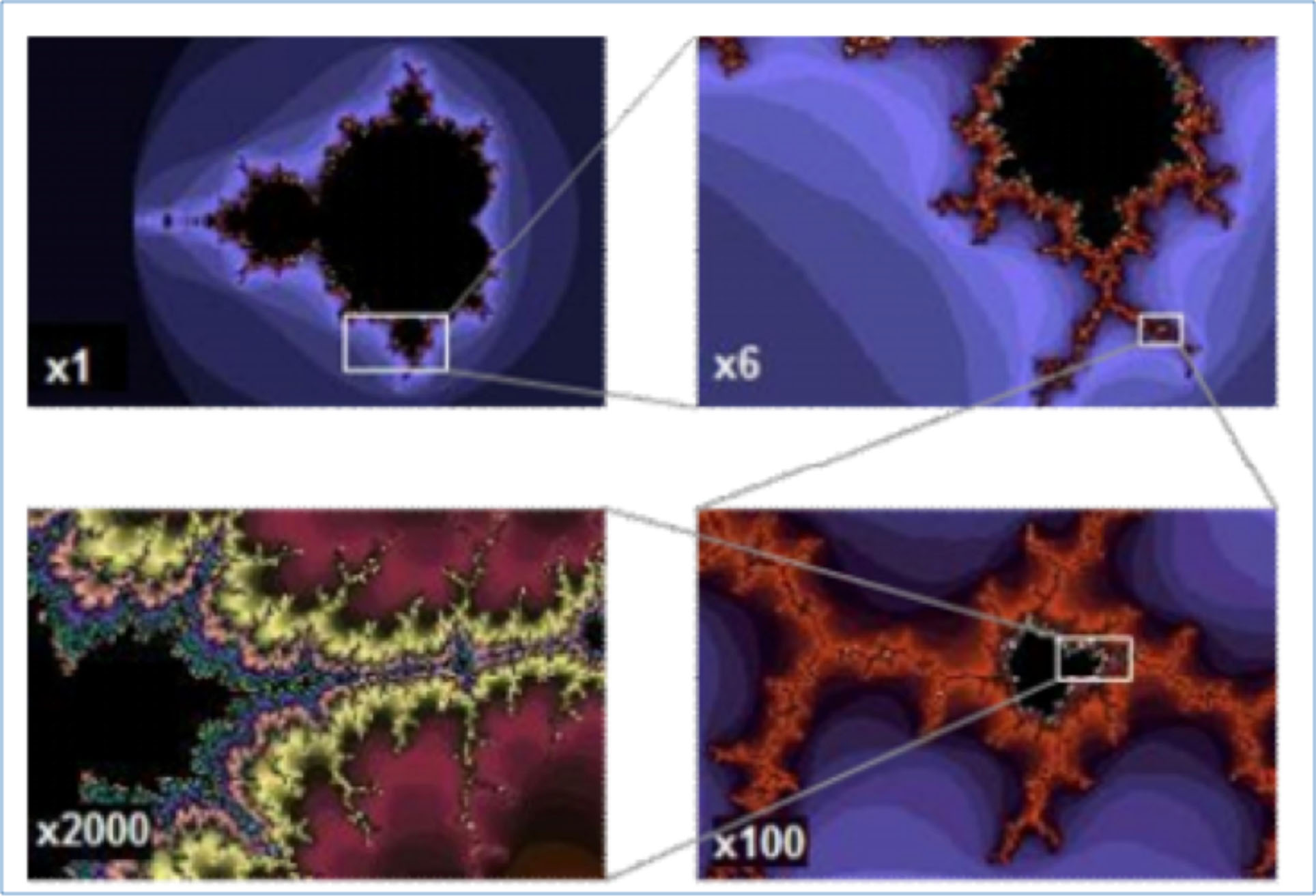
Şekil 2. Mandelbrot Dizisinin 2000 Kez Büyütülmüş Hali (Ortaya Çıkan İnce Detaylar Bütün Diziye Benzemektedir)
İnsan eliyle planlama…
Kısmi çözümleme karakteristikleri aynı zamanda bulutlar, dağlar ve ağaçlar gibi doğal nesnelerde de bulunabilir. Kısmi analizler; doğadaki bağlantıların ortaya çıkarılması için de şekillendirilebilirler. Bir kent; insan eliyle planlanıp yapılabilir ve aynı zamanda insan etkinlikleri ve doğadan da derin bir şekilde etkilenebilir. Araştırmalar; boru hatları ağı, karayolu ağları, arazi kullanımı ve insan yerleşimleri gibi birçok alt sistemler ile bunların kısmi karakteristiklerini birbiri ile uyumla barındıran bir kenti ortaya çıkarmaktadır. Bunun örneği Şekil 3’te verilmiştir. Genel anlamda bir kentin ana arter ağına sahip olduğu ve bu arterlerin her birisinin de sürekli olarak tali karayollarına bağlandığı gerçeği, bir evin içerisinde bile görülmeyen bir yürüme yolu izleri olduğu mantığı ile birleştirilebilir. İstatistiksel kendine benzerlik arka planda bu fenomeni yapısal bir karakteristik olarak bulundurmaktadır.


Şekil 3. Kısmi Çözümleme Karakteristiklerini Taşıyan Bir Kentsel Ulaştırma Ağı
Hepinize sağlıklı huzurlu mutlu ve başarılı günler dilerim.






